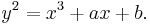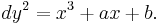Twists of curves
In mathematics an elliptic curve E over a field K has its quadratic twist, that is another elliptic curve which is isomorphic to E over an algebraic closure of K. In particular, an isomorphism between elliptic curves is an isogeny of degree 1, that is an invertible isogeny. Some curves have higher order twists such as cubic and quartic twists. The curve and its twists have the same j-invariant.
Contents |
Quadratic twist
Let E be an elliptic curve over K of the form:
Given 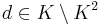 and
and 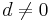 , the quadratic twist of E is the curve Ed, defined by the equation:
, the quadratic twist of E is the curve Ed, defined by the equation:
The two elliptic curves E and Ed are not isomorphic over K, but over the field extension K(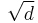 ).
).
Quartic twist
It is possible to "twist" elliptic curves with j-invariant equal to 1728 by quartic characters; twisting a curve E by a quartic twist, one obtain four curves: one is isomorphic to E, one is its quadratic twist, and only the other two are really new. Also in this case, twisted curves are isomorphic over the field extension given by the twist degree.
Cubic twist
Analogously to the quartic twist case, an elliptic curve over K with j-invariant equal to zero can be twisted by cubic characters. The curves obtained are isomorphic to the starting curve over the field extension given by the twist degree.
Examples
3.Twisted tripling-oriented Doche–Icart–Kohel curve
References
- P. Stevenhagen (2008). Elliptic Curves. Universiteit Leiden. http://websites.math.leidenuniv.nl/algebra/ellcurves.pdf.
- F. Gouvea, B.Mazur (1991). The square-free sieve and the rank of elliptic curves. Journal of American Mathematical Society, Vol 4, Num 1. http://www.ams.org.proxy.library.uu.nl/jams/1991-04-01/S0894-0347-1991-1080648-7/S0894-0347-1991-1080648-7.pdf.
- C. L. Stewart and J. Top (1995). On Ranks of Twists of Elliptic Curves and Power-Free Values of Binary Forms. Journal of the American Mathematical Society, Vol. 8, No. 4 (Oct., 1995), pp. 943–973. http://www.jstor.org.proxy.library.uu.nl/stable/pdfplus/2152834.pdf.